Un automate de Collatz est constitué d’une grille unidimensionnelle dont les lignes verticales, appelées barres, peuvent recevoir ce que je nomme un pion (par analogie avec le plateau d’un jeu). La grille n’a pas nécessairement d’origine ni de longueur définie. Le premier pion peut être posé sur n’importe quelle barre.
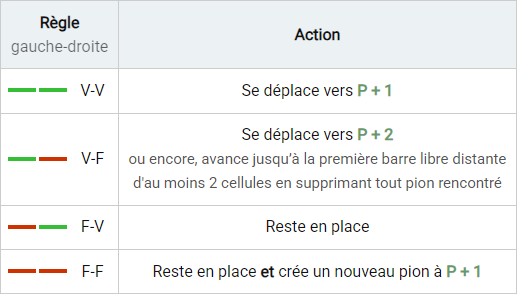
Les pions délimitent des groupes d’au moins une cellule (les premier et dernier pion représentent une exception. Voir ci-dessous). Le nombre de cellules que compte chacun des deux groupes entourant un pion définissent le voisinage de celui-ci.

- Les données du tableau sont exprimées en nombre de cellules.
- Un déplacement s’effectue vers la droite. Si sa valeur est 0 le pion ne bouge pas.
- Les opérateurs ≤ et ≠ expriment le fait que le premier et le dernier pion sont considérés comme ayant pour voisin de gauche, respectivement de droite, un groupe de 0 cellules. ≠ 1 peut en effet signifier 0.
- Création : le 1 signifie que dans ce cas on ajoute un nouveau pion une cellule à droite (c’est-à-dire sur la barre suivante). C'est la seule manière de créer un pion.
- Suppression éventuelle (indiquée par une croix rouge) : lorsqu'un pion se déplace de 2 cellules et tombe sur une barre déjà occupée, il remplace le pion qui s'y trouve et avance d’une cellule. Si sa nouvelle destination est également occupée, le même procédé se répète. En d’autres termes, le pion en mouvement ne s’arrête que lorsqu’il tombe sur une barre non occupée, après avoir supprimé tous les pions rencontrés.
Les déplacements s’effectuent en commençant par le dernier pion, puis l’avant-dernier, etc., jusqu’au premier. L’ensemble des déplacements est nommé une itération, à l’issue de laquelle l’automate se trouve dans un état différent de son état antérieur. Une itération étant basée sur l’état de l’automate avant qu’elle ne débute, donc sur le voisinage initial de chaque pion, lorsque l’un d’eux est déplacé le voisinage de son prédécesseur n’est pas altéré. On peut représenter ceci en ajoutant des pions fantômes, ou guides :

Le pion rouge vient d’être déplacé de deux cellules. C’est maintenant le tour du pion bleu, mais la valeur de son déplacement sera basée sur un groupe de droite de une cellule, non pas trois. Vous devez vous appuyer sur les guides pour déplacer les pions.
Exécuter une itération de l’automate revient à faire 3N+1 suivi de une ou plusieurs divisions par 2. Dans les deux cas on obtient le successeur impair de N dans une suite de Collatz. Comment procède-t-il ?
Le nombre de fois que 3N+1 peut être divisé par 2 correspond donc au nombre de cellules dont le premier pion s'est déplacé.
A l'issue de chaque itération, l'application affiche la nouvelle valeur de N ainsi que la liste d'exposants de 2 (virtuels) correspondant à la position de chacun des pions relativement au premier. Notez que cette valeur relative entraîne le fait qu'un déplacement de k cellules du premier pion décrémente automatiquement l'exposant de tous ses successeurs de k unités. Si vous avez déplacé manuellement un ou plusieurs pions, cliquez sur "Données actuelles" pour que s'affichent les données correspondant à l'état en cours de l'automate.
NB : les données en question sont calculées au moment de leur affichage en fonction de la position des pions. Il est important de comprendre que l'automate ne les utilise pas dans le cadre de son fonctionnement. Il n'utilise en fait aucune donnée, c'est un processus purement mécanique, comme si on le mettait en œuvre à l'aide d'une grille sur laquelle on aurait disposé des pions de Dames.
Cet automate est la troisième étape d’un travail de recherche dont on peut trouver le détail et les outils de calcul sur cette page. La colonne "Différences" est à l'origine de ma réflexion sur la possibilité d'en déduire un ensemble de règles qui les rendrait indépendantes des exposants, celles appliquées à ces derniers conduisant à un algorithme inutilement compliqué (colonne "Transformations").